Gerando Números Aleatórios
Esse artigo pretende introduzir o funcionamento e os tipos de algoritmos que fazem a geração de números randômicos.
[ Hits: 10.261 ]
Por: Pablo Margreff em 25/06/2015 | Blog: https://pmargreff.wordpress.com/
Os primórdios
Método do meio quadrado
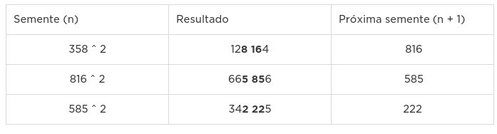
Sendo proposto por John von Neumann, esse foi o primeiro algoritmo para a geração de números aleatórios. Nesse método geramos um número de n dígitos, então pegamos uma semente com o mesmo tamanho de dígitos e à elevamos ao quadrado, depois pegamos os seus n dígitos centrais e também os elevamos ao quadrado, e continuamos repetindo o processo. Não existe problema em o número ter tamanho impar, basta fixarmos um lado para o corte.Exemplo (número aleatório de três dígitos):
Semente - 358 E assim sucessivamente até quando se desejar.
Nesse método temos dois problemas, o primeiro é que a sequência se repete em intervalos não muito grandes. O segundo é que para alguns casos, se gerarmos o número "zero" para um dos números que irá compor a próxima semente os números irão se transformar em zero.
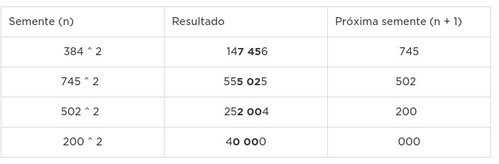
Exemplo (número aleatório de três dígitos):
Semente - 384 Como essa solução é determinística toda vez que usarmos a mesma semente teremos o mesmo número. Porém como a semente não é visível ao usuário a sensação transmitida é de aleatoriedade. O tamanho máximo de dígitos para a semente deve ser de 5 dígitos para a valores de 32 bits ou 15 dígitos para valores de 64 bits.
Método do meio do produto
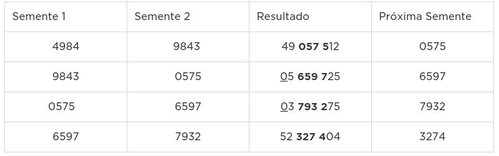
Esse método é parecido com o anterior, porém ao invés de usarmos uma semente iremos utilizar duas sementes de mesmo tamanho, e precisamos multiplicar essas sementes para obtermos um novo valor. Pegamos os n números centrais para gerar a nova semente, e multiplicamos com a semente anterior (na primeira iteração podemos escolher uma das duas sementes iniciais).A diferença é que agora os dígitos usados precisam ser os centrais. Para sementes que tem tamanho impar, precisamos de tamanho total impar no resultado, e para sementes de tamanho par, precisamos de resultados de tamanho par, se isso não acontecer podemos adicionar zeros à esquerda.
Exemplo (número de quatro dígitos):
Sementes: 4984 e 9843 Este método é mais eficiente que ao anterior pelo fato de repetir os números gerados em uma regularidade muito menor.
Estes algoritmos dificilmente são implementados hoje em dia pela sua previsibilidade alta.
Fontes:
- Sistema Galileu de Educação Estatística
- http://www.feferraz.net/files_/lista/random_numbers.pdf
- Revista programar edições 31 e 32, Geração de números aleatórios por Augusto Manzano
2. Os primórdios
3. Atualidade
Manipulação de imagens no formato PPM
Aumentando sua produtividade com o teclado padrão Dvorak
Upload Seguro de Arquivos em Aplicação Backend com Spring Boot, ClamAV e JWT
Instalação do Java da Oracle em distros Debian-like
Busca corporativa com Apache Solr - Motivação e conceitos
Conectando com Bco Interbase/Firebird em Java
Instalação e Configuração do JDK 7
é excelente esse artigo. favoritado!
se ainda houvessem notas para os artigos, 10 para esse!
Não sou da área, mas fica uma sugestão.
em um segundo artigo, se tiver tempo, revise, teste e classifique diversos
pacotes já existentes para gerar números aleatórios.
¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨
Albfneto,
Ribeirão Preto, S.P., Brasil.
Usuário Linux, Linux Counter: #479903.
Distros Favoritas: [i] Sabayon, Gentoo, OpenSUSE, Mageia e OpenMandriva[/i].
[1] Comentário enviado por albfneto em 25/06/2015 - 12:44h
é excelente esse artigo. favoritado!
se ainda houvessem notas para os artigos, 10 para esse!
Não sou da área, mas fica uma sugestão.
em um segundo artigo, se tiver tempo, revise, teste e classifique diversos
pacotes já existentem para gerar números aleatórios.
¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨
Boa sugestão, talvez agora nas férias isso aconteça.
Muito interessante o artigo, poderia ter exibido alguns códigos geradores de números aleatórios. Outra dica seria o uso desses geradores no Método de Monte Carlo.
O algoritmo Rho-Pollard também gera uns aleatórios, exceto por uma característica cíclica que o transforma em um fatorador.
--
http://s.glbimg.com/po/tt/f/original/2011/10/20/a97264_w8.jpg
Encryption works. Properly implemented strong crypto systems are one of the few things that you can rely on. Unfortunately, endpoint security is so terrifically weak that NSA can frequently find ways around it. — Edward Snowden
Patrocínio
Destaques
Artigos
Berry Bank: Criando um Banco Digital Gamificado para seus Filhos com Gentoo, Flask e Tailscale
Papagaiando o XFCE com temas e recursos
Dicas
Instale o DOOM Retro no Gentoo facilmente via Overlay
Steam (Flatpak) rodando jogos em partição NTFS
O dock Plank + U-Launcher deixam qualquer desktop mais produtivo
Tópicos
Instalar Linux em notebook Sony Vaio VPCEG13EB (17)
Alguém tem que acabar com ANATEL!!! (10)
O que você está ouvindo agora? [2] (229)
Top 10 do mês
-

Xerxes
1° lugar - 129.078 pts -

Fábio Berbert de Paula
2° lugar - 59.363 pts -

Buckminster
3° lugar - 27.907 pts -

Sidnei Serra
4° lugar - 21.261 pts -

Alberto Federman Neto.
5° lugar - 20.932 pts -

Alessandro de Oliveira Faria (A.K.A. CABELO)
6° lugar - 20.013 pts -

Mauricio Ferrari (LinuxProativo)
7° lugar - 19.760 pts -

edps
8° lugar - 18.897 pts -

Daniel Lara Souza
9° lugar - 18.848 pts -

Andre (pinduvoz)
10° lugar - 17.137 pts