Método de Newton e PHP

laudelino7

O método de Newton é um método matemático que pode ser utilizado para resolver equações. Como este método pode ser descrito em forma de algoritmo, então ele é facilmente aplicado à linguagem PHP (ou qualquer outra linguagem de programação).

[ Hits: 104.502 ]

Por: Laudelino em 11/08/2004

0 0

Denuncie Favoritos Indicar Impressora

Aplicação à linguagem PHP

Primeiro devemos definir uma função (equação) de que queremos calcular a raiz. Por exemplo:

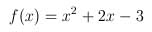
$f(x)=x^{2}+2x-3$

Em PHP está função fica da forma:

function funcao($x) {
$fx = pow($x,2) + 2*$x - 3;
return $fx;
}

Agora que definimos a função, devemos definir sua derivada:

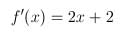
f'(x)=2x+2

Em PHP:

function derivada($x) {
$flinhax = 2*$x + 2;
return $flinhax;
}

Com a função e sua derivada prontas, iremos construir o algoritmo (já em linguagem PHP) que determina o método de Newton.

function metodo_de_newton($x) {
   $funcao = funcao($x);
   $derivada = derivada($x);
   $xi_mais_1 = $x - $funcao/$derivada; // Este é o algoritmo!
   return $xi_mais_1;
}

Devemos definir o número máximo de repetições e o valor inicial e colocar o algoritmo para funcionar como a seqüência exibida na página anterior.

$L = 10; // Número máximo de repetições
$i = 0; // Valor da primeira repetição (poderia ser 1 também)
$xi = array(); // Valores da seqüência
$xi[0] = ??; // 1o. valor da seqüência, o ponto de partida, o valor inicial

Exibimos os valores obtidos com a primeira iteração:

echo "<table align=\"center\" border=\"1\">\n";

echo "<tr bgcolor=\"999999\"><td align=\"center\">n</td><td align=\"center\">x<sub>n</sub></td><td align=\"center\">f(x<sub>n</sub>)</td><td align=\"center\">f'(x<sub>n</sub>)</td><td align=\"center\">ERRO</td></tr>\n";

echo "<tr><td>0</td><td>" .$xi[0] . "</td><td>" . funcao($xi[0]) . "</td><td>" . derivada($xn[0]) . "</td><td align=\"center\">****</td></tr>\n";

Utilizamos um comando "while" para que o método se repita até o número máximo de repetições, ou quando achar o zero da função, ou o valor da derivada for zero:

while ($i < $L) {
   if (flinha($xn[$i]) == 0 || funcao($xn[$i]) == 0) {
      $i = $L + 1;
   } else {
     $xn[$i+1] = algoritmo($xn[$i]);   // Sequência exibida na página anterior!
     $erro = abs($xn[$i+1] - $xn[$i]); // Calcula o valor do erro nas aproximações,
                                // para saber mais sobre o cálculo do erro
                               // consulte a referência [3].
     echo "<tr><td>";
     echo $i+1;
     echo "</td><td>" . $xn[$i+1] . "</td><td>" . funcao($xn[$i+1]) . "</td><td>" . flinha($xn[$i+1]) . "</td><td>$erro</td></tr>\n";

     $i = $i + 1;
    }
}
echo "</table>"; // Para "fechar" a tabela que abrimos.

Nossa aplicação em PHP do método de Newton está pronta. Na próxima página você terá todo o código já pronto para o uso.

OBS: Esta aplicação só calcula raízes reais. Deve-se organizar o algoritmo para que ele possa calcular raízes imaginárias.

Página anterior Próxima página

Páginas do artigo

   1. Introdução
   2. O método de Newton
   3. Aplicação à linguagem PHP
   4. newton.php
   5. Pequeno comentário sobre o código PHP
   6. Conclusão
   7. Referências

Outros artigos deste autor

PostgreSQL: comandos básicos

Programando PostgreSQL + PHP

Criptografando mensagens com PHP

Leitura recomendada

Utilizando PEAR

Trabalhando conteúdo dinâmico com Smarty

Aumente sua produção em PHP

Organizando projetos com a classe FastTemplate (parte 1)

Relatórios com PHP e XSLT - Conceitos iniciais e utilização básica

Comentários

[1] Comentário enviado por removido em 11/08/2004 - 16:02h

parabéns pelo artigo.....

fazia algum tempo q nao via nd desses lances...... :)

falo veio t+

0 0

[2] Comentário enviado por mafioso em 12/08/2004 - 15:46h

Tive que fazer um algoritmo como o seu... Mas o meu algoritmo não era baseado em difinir um número de iterações, mas sim um erro (erro = xn - x[n-1]). Fiz tanto o método de Newton como o método da Bissecção (um método parecido). As saídas do algoritmo estão em:

www.noclique.com.br/calculo/newton.php (método de Newton)
www.noclique.com.br/calculo/bisseccao.php (método da Bissecção)

Se alguém quiser ou precisar destes algoritmos, é só me pedir!

Valeu pelo artigo!

0 0

[3] Comentário enviado por rafa_mat em 13/08/2004 - 10:44h

Eu fiz um um algoritmo em C para um trablho da faculdade, que calcula o método de Newton Modificado para raízes multiplas com qualquer função de grau <= 6. Tb fiz uma versão pra kylix. Se alguém quiser, é só pedir tb!!! Ficou muito legal o artigo!! Parabéns!!!

3 0

[4] Comentário enviado por birilo em 15/08/2004 - 10:52h

Coloca como script aqui Mafioso

0 0

[5] Comentário enviado por hvasoares em 24/12/2005 - 05:52h

Newton é um método ótimo para resolver equações, mas infelizmente você vai ter que conhecer a derivada da equação que lhe interessa (há derivadas monstruosas).
Dêem um pesquisada na internet sobre esse método e vocês verão que ele é realmente muito interessante, pois não é preciso usar derivadas. Eu tenho um implementação em C++, a quem interessar e-mail-me.

1 0

[6] Comentário enviado por mafioso em 23/02/2007 - 23:33h

Como me pediram, atualizei o link com as saídas dos algoritmos do método da bissecção e do método de newton. Além disso, disponibilizei os códigos fonte neste arquivo:

http://www.noclique.com.br/calculo/calculo.zip

0 0

[7] Comentário enviado por civicx em 27/02/2007 - 21:54h

Opa.. muito bommm..!!

Eu tb estou atrais de um em Java, que eu entendo melhor a linguagem..

vc sabe onde eu consiga esses metodos em JAVA?

MUITOO obrigadoooooooo ;)

0 0

[8] Comentário enviado por removido em 20/12/2007 - 19:21h

Boas,
Estou a colocar este Help porque estou mesmo a necessitar de ajuda. Estou no último ano da minha Licenciatura e preciso de apresentar um trabalho onde tenho de implementar os seguintes metodos em linguagem C:
• Equações não lineares
o Método da Secante
o Método de Newton
• Sistemas de equações lineares
o Método de gauss-seidel
• Sistemas de equações não lineares
o Método de Newton
• Optimização Unidimensional
o DSC
• Optimização Multidimensional
o Nelder-Mead
o Quasi-Newton (versão BFGS) com critério de Armijo na procura do valor de alfa
Não estou a conseguir reunir informação para conseguir implementar os metodos e começo a ficar preocupado porque posso não terminar meu curso devido a esse trabalho.
Alguém sabe indicar-me onde posso encontrar informação sobre os codigos ou a forma como posso implementar os algortimos?
Fico muito agradecido a quem me puder ajudar.
Obrigado
Francisco

0 0