Fundamentos da criptografia assimétrica
Algorítimos assimétricos, mais conhecidos como de "chave pública e privada", são baseados em alguns princípios matemáticos considerados inexistentes, até que o "tolo" Whitfield Diffie conseguiu o que todos julgavam impossível, inaugurando uma nova era de cifras. Este artigo descreve esta história e como "Deus recompensa os tolos!".
[ Hits: 151.173 ]
Por: Elgio Schlemer em 03/08/2009 | Blog: https://elgio.prof.nom.br/~elgio
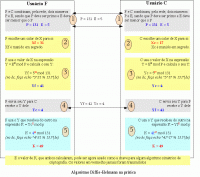
Algoritmo Diffie-Hellman
Porém, como números grandes demandam operações aritméticas gigantescas, irei demonstrar o funcionamento do algoritmo usando números pequenos, para que todos possam reproduzir em suas calculadoras de linha de comando bc!
O algoritmo de troca de chaves Diffie-Hellman constitui em uma série de operações matemáticas feitas por ambas as partes, sendo que ambos chegarão a um mesmo valor, a um mesmo número. Este número pode ser usado, então, como chave para algum algoritmo simétrico. Ele permite compartilhar uma única chave entre duas partes mas sem jamais enviá-la pela rede e sem possibilidade de alguém a descobrir.
Consiste nas seguintes etapas, feitas por ambas as partes:
- Ambos, em conjunto, escolhem dois números que não serão segredos, o número P e E. P deve ser um número primo e E deve ser menor que o P.
- Cada um escolhe para si um número X, mantendo-o em segredo
- Cada um usa o seu valor de X na operação modular, envolvendo P e E. Obtém com isto um número que chamaremos de Y
- Cada um envia para o outro o seu valor de Y
- Cada um realiza novamente a operação de módulo, porém usando o Y que recebeu do outro. Magicamente ambos obterão o mesmo resultado.
Confuso? Acredito que um exemplo completo, com operações e valores reais ajude na compreensão. Com números pequenos ainda se é vulnerável ao ataque por força bruta, pois o atacante, não tendo nenhum dos valores de X, poderá tentar usar alguns possíveis valores até acertar. Porém se usar números realmente grandes, da ordem de 512 bits, o número de tentativas torna inviável este ataque.
2. A utopia da troca de chaves de forma segura
3. Os "tolos" venceram
4. Algoritmo Diffie-Hellman
5. Conclusão
Autenticação por desafio e resposta no SSH
Criptografia assimétrica com o RSA
Armazenamento de senhas no Linux
Criptografia chave simétrica de bloco e de fluxo
Gerenciamento de segurança da informação com open source (parte 1)
Instalando o antivírus BitDefender no Linux
Procurando rootkits no seu sistema
Implementando segurança no SSH
Proteção utilizando fail2ban contra ataques do tipo
Muito bom seu artigo
principalmente para esclarecer algumas duvidas
de iniciantes como eu
Abraço...
Elgio,
Parabéns pelo artigo. Muito simples e direto, como uma boa aul deveria ser.... Estou estudando para prestar a poscomp e esse artigo veio bem a calhar...
Jeff
Cara
Artigo nota 10!!!
nunca vi um artigo sobre criptografia mais claro que esse.
Att,
Anthony Collucci
Estudei criptografia assimétrica quase fiquei louco, tem algorítimo muito complexo.
Ótimo artigo, Elgio. Passei a interessar-me mais pela criptografia, tanto que já estou pra ler o livro Cryptonomicon :-)
[ ]'s
Eu tentei aplicar esse algoritmo em PHP mas ele retorna incrivelmente -1
p=131 e=5 xf=31
pow(5,31)=4.65661287308E+21 % 131 = -1
<?php
$p=131;
$e=5;
$xf=31;
echo "p=".$p." --- e=".$e." --- xf=".$xf."<br>";
$yf = ( pow($e,$xf) % $p );
echo "pow($e,$xf)=".pow($e,$xf)." % ".$p." = ".$yf;
?>
Analisando mais profundamente o que acontece:
Considerando P=131 E=5 Xf=31 temos segundo o exemplo:
Yf = 5^31 mod 131 portanto temos:
5^31 = 4,656612873077392e+21
considerando Z = (5^13) / 131 temos Z = 3,554666315326253e+19
agora para pegar o resto temos que multiplicar assim Z*131 que dá 4,656612873077391e+21 e esse valor deve ser subtraído do 5^31, logo:
(5^31) - (Z*131) = ( 4,656612873077392e+21 - 4,656612873077391e+21 ) = 0
Pronto agora todos devem entender o quanto eu sou péssimo em matemática kkkkk no php dá -1, fazendo na mão, o resultado é zero.
Qual a mágica de obter Yf=41 ????
O php não é uma boa linguagem para estes cálculos.
Primeiro porque não é capaz de lidar, naturalmente, com números grandes http://www.vivaolinux.com.br/artigo/Programacao-com-numeros-inteiros-gigantes Então pode ter ocorrido um overflow na operação e tudo já dançou.
Segundo porque o operador de módulo do PHP não é realmente operador de módulo. É o operador de RESTO, que mesmo considerado como sinônimos eles NÃO SÃO!
-4 mod 10 deve dar 6 (-4 está a 4 posições antes do 10)
Mas no PHP, assim como no C, -4 mod 10 = -4
Teoria e detalhes em http://www.vivaolinux.com.br/script/Algoritmo-de-euclides-estendido-(calcula-o-D-RSA)
[]'s
Não de forma alguma, passei um tempinho estudando como fazer estes cálculos no PHP e ele possui uma biblioteca matemática para essas operações mais complexas, procurem na área de scripts do VOL por PHP > Segurança > diffiehellman vou postar lá:
p=131 e=5 xf=31 xc=17
e^xf => 5 ^ 31 = 2147483647 mod 131 = 41
e^xc => 5 ^ 17 = 2147483647 mod 131 = 4
kf = 49 kc = 49
agora só falta desenvolver o gerador de números primos.
otimo artigo com bastante fatos historicos mais nao acho q o tema foi adequado para o artigo.
parabens pelas informacoes colhidas
Muito bom o artigo!
Me tirou muitas dúvidas.
Obrigado.
Exelente artigo como todos que tenho lido aqui postados pelo Elgio,muito bacana um pessoa compartilhar de seus conhecimentos para que outros venham a aprender e conhecer melhor alguns conceitos de programação e etc...
"Deus recompensa os tolos!".-tvz como frase de efeito está OK,mas a tradução correta seria : Deus recompensa os sabios!!! que sao julgados tolos ^^
abraços brother
GOSTEI MUITO, MAS GOSTARIA DE EXPLICAÇÃO SOBRE A CRIPTOGRAFIA SKIPJACK.. FICARIA BEM GRATO...
LUZ PAZ E AMOR
Excelente artigo. Queria que você passe uma informação,
Esse algoritmo pode aplicado em java?
Já havia lido sobre o método de Rabin e o RSA. O algoritmo de Diffie-Hellman ainda não conhecia.
Parabéns pelos artigos.
Desculpe "Brown", mas...
Quem aqui disse que não era?
Existe um erro nisto tudo, a matemática é perfeita, ou seja existe sim uma forma de resolver esse algorítimo. Mas eu acho que a graça da criptografia é esta. AHahhAHAhaHahhaHahaha
A propósito na imagem está escrito manidos ao invés de mantidos.
Excelente artigo, parabéns e obrigado.
Muito bom seu artigo, gostei muito.
entao pode ser usando um tipo de divisão de polinômios no caso f(x)= Q(x)(x-a) + R(x), sendo (x-a) é a raíz no caso o divisor, f(x) a função o dividendo Q(x) o quociente e o R(x) o resto, no segundo caso também pode ser usado dessa maneira mas usando logaritmo no caso (xln(23)-ln(1311) = ln(1227) sei lah acho q isso ajudaria muito a utilizar um para decifrar certos, ou é somente matemática básica mesmo hehe
Não vi até hoje nenhuma explicação tão profunda e, ao mesmo tempo, tão cristalina, que me fizesse entender o princípio e os desdobramentos do mecanismo da criptografia.
Parabéns. Aliás, parabéns sempre!
Todos os artigos que você produz são muito bem escritos e elucidativos, obrigado por compartilhar conosco o seu vasto conhecimento.
Muito bacana o artigo. Sua didatica é excelente. Professores assim que o mundo precisa ^^
Achei super maneiro aquela ideia dos cadeados.
Mas eu queria fazer uma pergunta (me ocorreu exatamente agora)
na matemática (que é uma ciência exata) não deve existir (ou já existe) uma forma de desfazer esse modelo usado? Assim como a divisão anula a multiplicação, não teria um calculo pra anular os que foram realizados exemplos e descobrir os números em vermelho? (sem ser por tentativa e erro ou mesmo sendo, mas deixando pistas sobre os mais provaveis, dando pra reduzir uma lista de infinitas para algo mais possível)?
Fiquei com vontade de estudar criptografia só de ler este artigo.
Já tinha lido alguma coisa em outros lugares, mas o seu artigo ajudou a esclarecer mais esse assunto.
Muito bom.
Parabéns pelo artigo. Realmente interessante e muito bem feito. Claro e sucinto
muito bom! nas férias vou dar uma bela estudada em criptografia
??...??
Srs. PAra mim a criptografia ainda é um misterio.
Contudo este artigo me fez ter uma ideia, ainda não pragmatica do sistema.
Sou um analista em fase embrionaria...rsrs, contudo Gostei do assunto da criptografia!
Grande artigo. Passou a mensagem de forma clara, simples e direta. Parabéns.
O código que postaram lá em cima:
<?php
$p=131;
$e=5;
$xf=31;
echo "p=".$p." --- e=".$e." --- xf=".$xf."<br>";
$yf = ( pow($e,$xf) % $p );
echo "pow($e,$xf)=".pow($e,$xf)." % ".$p." = ".$yf;
?>
Isso deve ser enxuto, calculando multiplicação por partes e pegando o resto da divisão em cada etapa.
Assim os valores não chegarão a absurdos por causa de estouros dos valores.
Ótimo artigo, é muito bom sabe mais sobre a história e a criptografia na prática, além de ser uma assunto muito interresante.
Parabéns!
Elgio, parabéns pelo artigo!!!
O conteúdo é muito bom, claro e objetivo. Estou adorando ler todos os seus artigos que falam sobre a criptografia.
E obrigado por compartilhar um pouco do seu conhecimento!!!!
Patrocínio
Destaques
Artigos
A combinação de WMs com compositores feitos por fora
Audacious, VLC e QMMP - que saudades do XMMS
SUNO OpenSource: Crie um servidor de gerador de música com IA
Instalação Completa e Configuração Básica do Void Linux
A Fundação da Confiança Digital: A Importância Estratégica de uma PKI CA na Segurança de Dados
Dicas
Tenha opção de emblemas embutido no pcmanfm
Instalar o Microsoft Teams no Ubuntu e Derivados
Tópicos
O WiFi não reconhece minha rede depois que o processo de suspensão é r... (4)
Instalador não reconhece SSD Sata. (12)
Quero configurar cgconfig.conf (0)
Top 10 do mês
-

Xerxes
1° lugar - 130.372 pts -

Fábio Berbert de Paula
2° lugar - 60.963 pts -

Buckminster
3° lugar - 36.818 pts -

Alberto Federman Neto.
4° lugar - 26.430 pts -

Alessandro de Oliveira Faria (A.K.A. CABELO)
5° lugar - 20.200 pts -

Sidnei Serra
6° lugar - 19.870 pts -

Daniel Lara Souza
7° lugar - 19.363 pts -

Mauricio Ferrari (LinuxProativo)
8° lugar - 19.421 pts -

edps
9° lugar - 18.243 pts -

Andre (pinduvoz)
10° lugar - 14.748 pts